The relation between the decrease of mass and the energy that releases is given by
E = Δm.c2
- E energy in J
- Δm decrease in mass (mass defect) in kg
- c speed of light (in vacuum) in m.s -1 cvac = 2.99792458 x 108 m.s-1
Example
α-decay and the release of energy
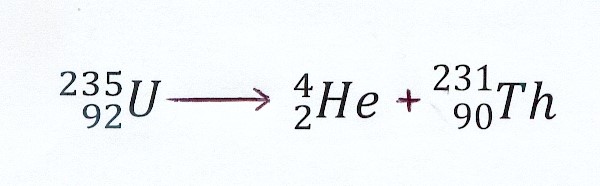
Atomic mass U-235 = 235.038893 u
Atomic mass He-4 = 4.002603 u
Atomic mass Th-231 = 231.03629 u
u : atomic mass unit
1 u = 1.66054 x 10-27 kg
We compare the mass before en after the disintegration
mass U-235 : 235.04393 u mass He-4 (α-particle) : 4.002603 u
mass Th-231 : 231.03629 u _
____________________
235.038893 u
Mass decreases with : 235.038893 u – 235.04393 u = 0.005037 u (mass defect)
Released Energy
E = Δm.c2 =( 0.005037 x 1.66054 x 10-27) (2.99792458 x 108)2 = 7.539315488 x 10-13 J =
4.7121 x 106 eV
Also possible:
E = 0.005037 x 931.49 = 4.6919 MeV
(1 u is equivalent with 931.49 MeV)
Remark
An atomic mass includes the mass of the orbital electrons. This causes no error, because the number of electrons included by U-235 is equal to the number of electrons of He-4 and Th-231.
Example
β– decay and the release of energy
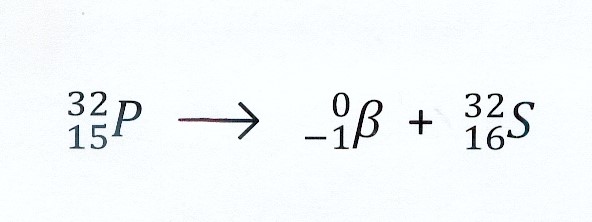
Before disintegration:
mass P-32 atom : 31.97391 u
mass 15 electrons : 15 x 0,00055 u = 0.00825 u _
—————————-
mass P-32 nucleus 31.96566 u
After disintegration
massa S-32 atom : 31.97207 u
massa 16 electrons : 16 x 0,00055 u= 0.0088 u _
—————————–
massa S-16 nucleus 31.96327 u
massa β– ( electron) 0.00055 u
Mass decreases with :
Δm =31.96566 u – ( 0.00055 u + 31.96327 u) = 31.96566 u – 31.96382 u = 0.00184 u
Released Energy
E = Δm.c2 =(0.00184 x 1.66054 x 10-27) ( 2.99792458 x 108)2 = 2.74605 x 10-13 J = 1.7163 x 106 eV =
1.7163 MeV
