One dimensional motion

<v>= Δx/Δt       

• <v>    average velocity  in ms^-1
• Δx      displacement  in m  (x final position minus x initial position)
• Δt       elapsed time in s

Example

Someone runs 100 m in 15 s. Then he runs  40 m back in 10 s.

Find the average velocity.

<v>= Δx/Δt      = 60 (!) / 25 = 2.4 m/s

One-dimensional motion with constant velocity

Δx = v Δt       x – x₀ = v t       s=v t      

One-dimensional motion with constant acceleration 

a = Δv/Δt                               v = V₀ + at

• Δv       final velocity minus initial velocity  in ms^-1
• a         acceleration  in ms^-2
• v₀        initial velocity in ms^-1

 Δx = v₀t + ½at²            x = x₀ + v₀t + ½at²         s = v₀t + ½at²                        

Examples

1. A car accelerates from rest to a velocity of 90 km/h in 15 s.

     Find the displacement during this time.

     v  = 90 km/h = 25 m/s

a = Δv/Δt = (25-0)/(15-0) = 1.67 ms^-2    

s = ½ a t² = ½ 1.67 15² = 188 m = 1.9 x10² m

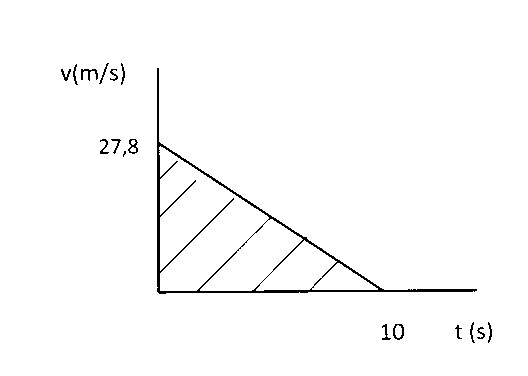
2. A car with a velocity of 100 km/h  is braking and stopped after 10 s

     Find the displacement during these 10 s.

     The initial velocity is 100 km/h = 27.8 m/s

     You can calculate the stopping distance in different ways

a. For a movement with constant acceleration  we may write:

  <v>= (v₁ + v₂)/2 = (27.8 + 0)/2 = 13.9 m.    s = <v> t = 13.9 x 10 = 139 m = 1.4.10² m

b. a = Δv/Δt   =  (0 – 27.8)/10 = – 2.78 m/s²    (velocity decreases)

s = v₀ t + ½ a t² = 27.8 x 10 + ½ x – 2.78 x 10² = 278 – 139 = 139 m = 1.4.10²  m

c. The displacement is equal to the area under a velocity –time graph     ( the shaded area in the drawing )                                    

s = ½ x 27.8 x 10 = 139 m = 1.4.10² m