W = F s cos α
- W work in J (Joule) (not to be confused with the weight)
- F force in N
- s displacement in m
- α angle between F en s
Example 1

See the figure. On an object acts a force F. The object moves 100 m to the right.
The angle α between F and the x-direction is 35 o. The weight is 30 N.
Also work on this object a frictional force (f=5.0 N) and a normal force Fn.
a.Find the work of F
Resolve F in the x-direction (parallel to the displacement) and in the y-direction (perpendicular to the displacement)
F x = 16.4 N (Calculation : cos 35 o = Fx/ F Fx = F cos 35 o)
WF = Fx s = (16.4)( 100) = 1640 J
Also possible : W = F s cos α = (20)( 100 cos 35) = 1640 J
Remark
If force and displacement have the same direction : W > 0 J
b. Find the work of the frictional force f
Wf = – f s= – (5.0)(100) = – 500 J
of
Wf = f s cos α =(5.0)( 100 cos 180o) = (5.0)( 100)( -1) = – 500 J
( If force and displacement are oppositely directed then W < 0 J)
c. Find the work of weight and normal force
W w= W Fn = 0 J
( If F ┴ s then : W = 0 J, α= 90o cos 90o = 0)
Example 2
An object with a mass of 5.0 kg falls 20.0 m downward.
How much is the work of the weight ?
W = m g = (5.0)( 9.81) = 49.05 N
Ww= W s = (49.05)( 20.0) = 981 J = 9.8 x 102 J
Example 3
we pull a spring ( k = 50 Nm -1) 20 cm.
Calculate the work done by the force excert by the spring.
Method 1
If the spring has been pulled to the right, the force in the spring is directed to the left.
Thus the work of Fspring is negative .
WFspring = – ½ k x2 = – ½ (50)(0.20)2 = – 1.0 J
Method 2
Determine work with F versus x graph
F = k x = (50)( 0.20) = 10.0 N
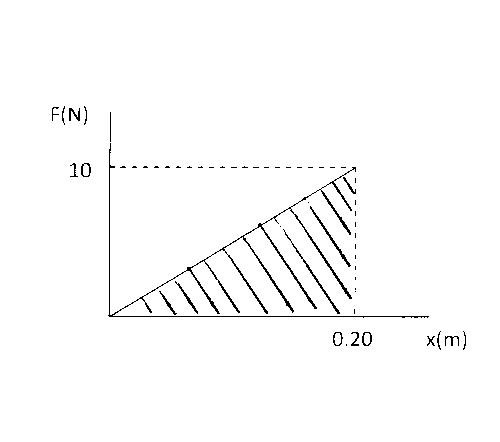
W is equal to the arae under the graph of F versus x
W = ½ (10.0)( 0.20) = – 1,0 J.
W < 0 because the force of the spring and displacement are oppositely directed.
